Ch06. Open Methods

Bracket method와는 달리 Open Methods는 근에 대해 수렴한다는 보장이 없다. 즉, 발산할 수도 있다는 뜻이다.

하지만, Open Methods를 사용하는 이유는 이것이 좀 더 빠르기 때문이다.

 

(a)는 이분법(수렴), (b)와(c)는 같은 방법을 사용하지만, 초기 추측에 의해 수렴/발산 여부가 정해진다.

 

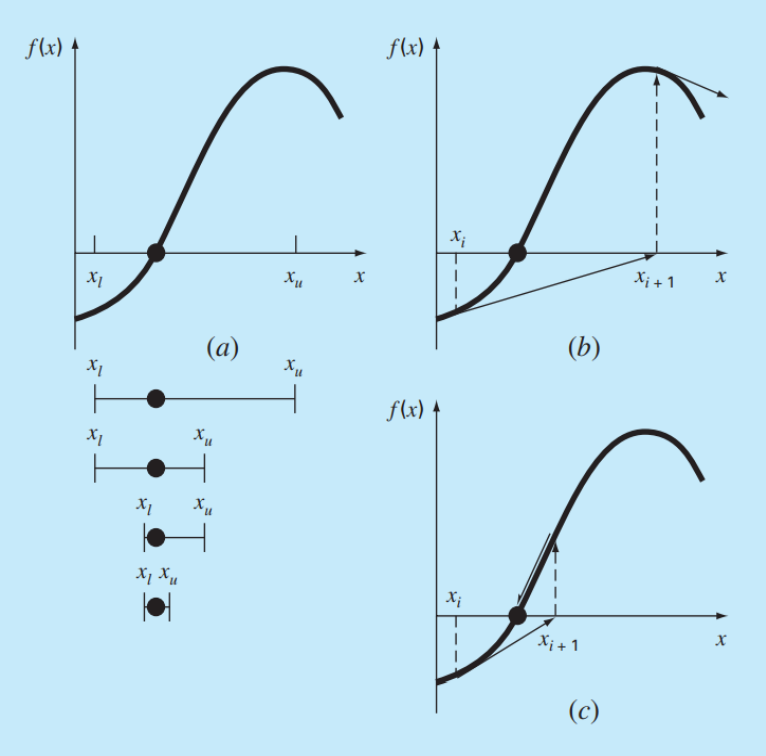
6-1. Simple Fixed-Point Iteration

f(x) = Someting eqution => f(x) = g(x)

y = f(x), y = g(x)

원래, f(x) = someting equation인데, 함수 f(x)를 x에 대한 방정식으로 바꿔서, 함수 2개가 만나는 지점으로 방정식의 근을 구하는 방법이다.

f(x) = x^2 - 3x + 4, x = (x^2 + 4) / 3

따라서, g(x) = x, f(x) =  (x^2 + 4) / 3

g(x) = f(x) 를 만족시키는 근을 찾아보자(위의 그래프 내용)

 

모든 방정식들이 고정점을 가지는 것은 아니다. 

예) y = x + 1과, y = x 이 둘은 서로 평행하기에 만나는 점이 없다.

 

예제1

예제1 풀이 방식

(a) f(x) = e^-x - x & g(x) = 0

(b) f(x) = e^-x & g(x) = x

 

근이 수렴/발산하는 사례들

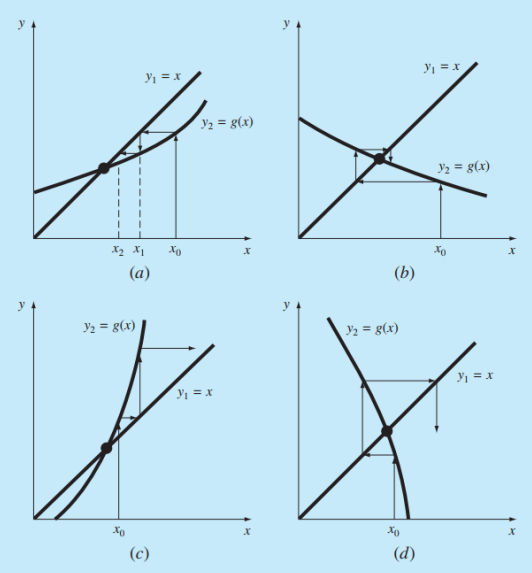
(a) & (c) = Monotone Pattern

(b) & (d) = Spiral Pattern OR Oscillating pattern

a와 b는 근에 수렴하는 방법 두 경우를 제외한 나머지 경우는 발산한다.

수렴하기 위해선 g(x)의 도함수의 절댓값이 1 보다 작아야한다.

 

Fixed-Point Seudo Code

 

6-2. Newton Raphson Method

Newton-Raphson Method

Newton-Raphson Method Solution

뉴튼 방정식으로 풀었을 때, 훨씬 푸는 속도가 빠르다.

뉴트 방식으로 푼 것을 잘 보면, 제곱승수 만큼 오차가 줄어드는 것을 볼 수 있다.

뉴튼 방정식으로 작성했을 때, 수렴이 잘 되지 않는 경우

 

6-3. The Secant Method

Backward finit divided difference ->(substitution) Newton-Raphson Method

 

뉴튼 방정식 방법은 어떤 한 점의 도함수의 기울기이지만, Secant방법은 어떠한 두 지점에 대한 기울기이다.

False position vs. Secant

6-3-3. Modified Secant  Method

기본 원리는 Secant와 동일하지만, 델타를 도입해서, xi+1와 x0사이의 간격을 최소화 시킨 기법

델타 값은 너무 작으면, 반올림 시 에러가 나고, 너무 크면, 분산의 우려가 있다(델타 값은 자동으로 정해지지 않는다.)

각 반복 횟수에 따른 오차율의 감소

 

6-4. Brent's Method

Bisection method와 Open Method결합

(b) Inverse

 

y = f(x)는 x축과 교차하는 점이 없지만, Inverse된 x = f(y)는 x축과 교차하는 지점이 있다.